Problems
Contain
- a general description of all its params, and
- a statement of what propaearties the solution, is required to satisfy.
An instance
of the problem: specifying particular params.
Example: Traveling Saleman Problem
Params:
- $C = \{c_1, \dots, c_n\} \rightarrow$ cities.
- $d(c_i, c_j)$.
Solution:
- an ordering $<c_{\pi(1)}, c_{\pi(2)}, \dots, c_{\pi(m)}>$ of cities that minimizes
$$
[\sum_{i = 1}^{m - 1} d(c_{\pi(i)}, c_{\pi(i + 1)})] + d(c_{\pi(m)}, c_{\pi(1)})
$$
ℹ️
a tour starts at $c_{\pi(1)}$, visits each city in sequence, then back to $c_{\pi(1)}$ from $c_{\pi(m)}$
One instance:
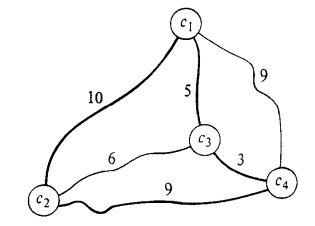
- $C = {c_1, c_2, c_3, c_4}$.
- $d(c_1, c_2) = 10$, $\dots$
$\rightarrow$ a solution $<c_1, c_2, c_4, c_3>$.
Algorithms
General, step-by-step procedures for solving problems.
Think of them as being computer programs.
❗
An algorithm is said to solve a problem $\Pi$ if
- that algorithm can be applied to any instance $I$ of $\Pi$ and
- is guaranteed always to produce a solution for that instance $I$.
Intractable
A problem is intractable if it is so hard that no polynomial time algorithm can possibly solve it.
A problem has not been “well-solved” until a polynomial time algorithm is known for it.
Encoding Scheme
A way of representing problem instances using symbols, typically as string.
Algorithm operates on encoded inputs, not abstract objects $\rightarrow$ choice of encoding scheme affects SIZE of inputs (n).
Example
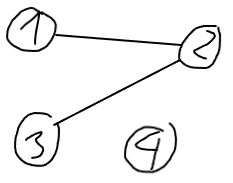
Graph $G = (V, E)$,
vertices $V = \{V_1, V_2, V_3, V_4\}$,
edges $E = \{(V_1, V_2), (V_2, V_3)\}$.
| Encoding Scheme |
String |
Length |
| Vertex list, Edge list |
V[1]V[2]V[3]V[4](V[1]V[2])(V[2]V[3]) |
36 |
| Neighbor list |
(V[2])(V[1]V[3])(V[2])() |
24 |
| Adjacency matrix rows |
0100/1010/0010/0000 |
19 |
Provably Intractable Problems
two different causes of intractability:
- Problems that require an exponential amount of time to solve
- typical definition of an intractable problem.
- Problems where the solution itself is too large to describe concisely
- might not be hard to compute, but their output is so vast that it cannot be expressed with a polynomial-length formula.
- Example: A variant of the Traveling Salesman Problem (TSP) where we want to find all tours with a total length $B$ or less.
- There could be an exponentially large number of valid tours shorter than B.
- No polynomial-time algorithm can list all of them.
explain
Since the saleman must visit every city exactly once, the number of possible routes: $(n - 1)!$
Say, even if half of them satisfy the B constraint, time complexity to explicitly list (n - 1)! routes is still
$$
\mathcal{O}(\frac{(n - 1)!}{2}) = \mathcal{O}(n!)
$$
Using Stirling's Approximation
$$
n! \sim \sqrt{2\pi n}(\frac{n}{e})^n.
$$
This grows faster than exponential time algorithm. Even if a polynomial-time algorithm exists to check whether a route is valid, writing down all valid routes would take an exponential amount of space.
The 2nd type can be regarded as a sign that the problem is not defined realistically, bc we are asking for more information than we could ever hope to use.
Thus, the focus is primarily on the first type: problems that requires exponential time to solve.
Undecidable Problems
Turing proved that
some problems are so hard that they are “undecidable”, in the sense that no algorithm can solve them at all.
Intractable but Decidable Problems
Meyer & Stockmeyer (1972) and Fischer & Rabin (1974).
Decidable but intractable problems have solutions, but they take exponential time using deterministic algorithms.

