Chapter 10 Exact Inference Clique Trees

Daphne Koller Nir Friedman probabilistic-graphical-models

Recall: The basic operation of the variable elimination algorithm is the manipulation of factors.

  • Multiplying existing factors $\to \psi_i$.
  • Eliminate variable $\to \tau_i$.

Consider $\psi_i$ as a computational data structure $$ \dots \to \psi_j \xrightarrow{\tau_j} \boxed{\psi_i} \xrightarrow{\tau_i} \psi_l \dots $$

  • takes “message” $\tau_j$.
    • generated by other factors $\psi_j$.
  • generates $\tau_i$.

Cluster Graphs

  • A cluster graph $\mathcal{U}$ is an undirected graph such that:
    • Each node is a cluster $C_i \subseteq \mathcal{X}$.
    • Each edge between a pair of cluster $C_i$ and $C_j$ is associated with a sepset (separator set) $S_{i, j} \subseteq C_i \cap C_j$.
  • Given set of factors $\Phi$, each factor $\phi_k \in \Phi$ must be assigned to one and only one cluster $C_{\alpha(\phi)}$ s.t. $Scope[\phi_k] \subseteq C_{\alpha(\phi)}$.
  • The initial belief of a particular cluster as a product of all the factors assigned to it: $$ \psi_i (C_i) = \prod_{\phi: \alpha(\phi) = i} \phi $$

Sum Cluster might have no factor $\to$ null product and is equal to 1.

one and only one?
  • It needs to be at least one so that the information is taken into account somewhere
  • and it shouldn’t be more than one because if given to more than one cluster, the evidence will be double counted.
Example: Assign factors
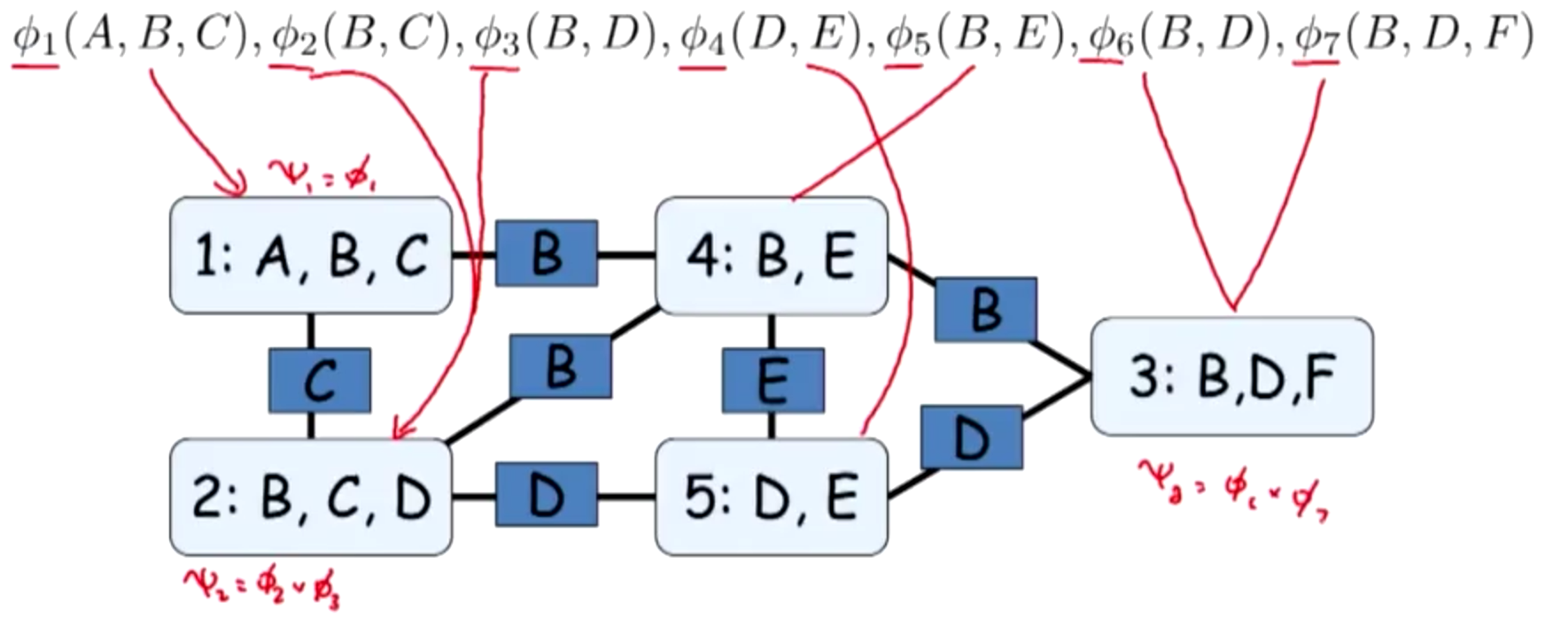
$\phi_2$ can go to both $C_1$ or $C_2$, this is just one possible way of assigning the factors to clusters.
Student Example
$$ \begin{align*} P(C, D, I, G, S, L, J, H) &= \phi_C(C) \phi_D(D, C) \phi_I(I) \phi_G(G, I, D) \phi_S(S, I) \\ &\quad \cdot \phi_L(L, G) \phi_J(J, L, S) \phi_H(H, G, J). \end{align*} $$

Student example

The message $\tau_1(D)$ generated from $\psi_1(C, D)$, participates in the computation of $\psi_2$: we have an edge from $C_1$ to $C_2$.

Properties of Cluster Graphs

Family Preservation

  • Given set of factors $\Phi$, each factor $\phi_k \in \Phi$ must be assigned to one and only one cluster $C_{\alpha(k)}$ s.t. $Scope[\phi_k] \subseteq C_{\alpha(k)}$. (In English: Each factor $\phi_k$ needs to be assigned to a cluster $C_{\alpha(k)}$ s.t. $C_{\alpha(k)}$ accommodate $\phi_k$).
  • For each factor $\phi_k \in \Phi$, there exists a cluster $C_i$ s.t. $Scope[\phi_k] \subseteq C_i$ (For each factor there’s a cluster accomodates $\phi_k$).

Clique Trees

The cluster graph associated with an execution of VE is guaranteed to have certain important properties.

  • VE used intermediate factor $\tau_i$ at most once $\rightarrow$ the cluster graph induced by an execution of VE is necessarily a tree because (there should be no cycle because if there’s more than one path from $C_i$ to $C_j$, $\tau_i$ will be used multiple times).
  • Although cluster graph is undirected, an execution of VE defines a direction for the edges (flow of messages between clusters).
    • The directed graph induced by the messages is a directed tree,
    • all the messages flowing toward a single cluster where the final result is computed.
    • This cluster is the root (not part of the definition of a cluster graph).

Clique Tree

  • Cluster tree such that:
    • nodes are clusters $C_i \subseteq \mathcal{X}$ (called cliques),
    • edges between $C_i$ and $C_j$ associated with sepset $S_{i, j} = C_i \cap C_j$,
    • satisfies the running intersection property.

Properties of Clique Tree

Family Preservation

  • Given set of factors $\Phi$, each factor $\phi_k \in \Phi$ must be assigned to one and only one cluster $C_{\alpha(k)}$ s.t. $Scope[\phi_k] \subseteq C_{\alpha(k)}$. (In English: Each factor $\phi_k$ needs to be assigned to a cluster $C_{\alpha(k)}$ s.t. $C_{\alpha(k)}$ accommodate $\phi_k$).
  • For each factor $\phi_k \in \Phi$, there exists a cluster $C_i$ s.t. $Scope[\phi_k] \subseteq C_i$ (For each factor there’s a cluster accomodates $\phi_k$).

Running Intersection Property (RIP)

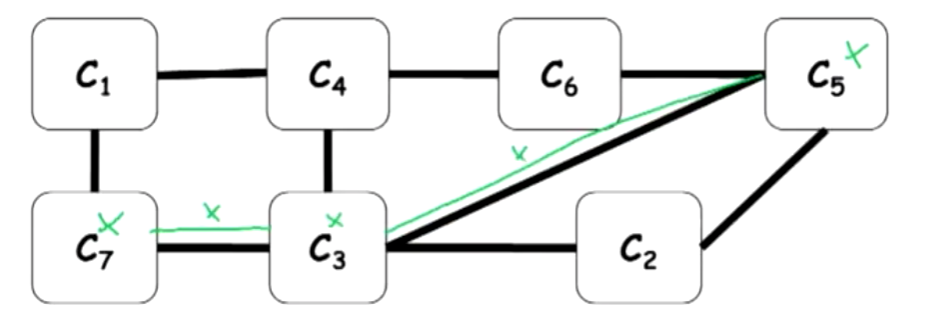
For each pair of clusters $C_i$, $C_j$ and variable $X \in C_i \cap C_j$, there exists a unique path between $C_i$ and $C_j$ for which all clusters and sepets contain $X$.

existence

Suppose $X \not\in S_{7, 3}$, there’s no way of $C_7$ to communicate to $C_3$ about the variable $X \rightarrow$ 2 seperate, isolated communities, each of which has some information about $X$ and they can never talk to each other about $X$, never going to get to agree about $X$.

That’s not very good, that path must exist.

uniqueness

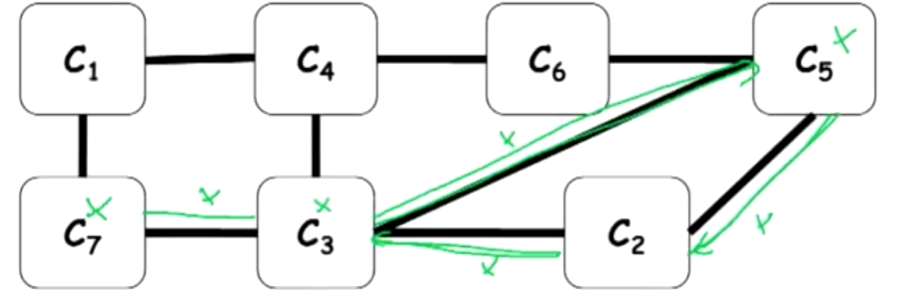
Suppose there’re 2 paths involved $X$.

Consider cycle $C_3 \to C_5 \to C_2 \to C_3$.

  • Suppose $C_3$ suggests that $X$ needs to take value 1, $C_5$ integrates with its own information and sends it to $C_2$ which sends it back to $C_3$.
  • Now, $C_3$ reinforces its beliefs that $X$ need to take the value 1 $\to$ the probability goes up.

This self-reinforcing loop is going to give rise to very extreme and skewed probabilities in many examples $\Rightarrow$ One way to reduce this risk is to prevent these kinds of feedback loops.

RIP implies $S_{i,j} = C_i \cap C_j$ If the cluster satisfies RIP, then shared variables between $C_i$ and $C_j$ must persist through the path between them. Thus, $S_{i, j} = C_i \cap C_j$.
an alternative view

For any $X$, the set of clusters and sepsets containing $X$ form a tree.

  • It has to be connected because of the existence of the path.
  • It can’t be a non tree because that would give us different paths.
𐰃𐰠𐰆𐰢
Let $\mathcal{T}$ be a cluster tree induced by VE over some set of factors $\Phi$. Then $\mathcal{T}$ satisfies the running intersection property.
  • $X$: a variable in the model.
  • $C$ and $C^{\prime}$: two clusters that contain $X$.
  • $C_X$: the cluster where $X$ is eliminated $\to$ the cluster where $X$ is summed out during VE.

Goal: prove that $X$ must be present in every cluster on the path between $C$ and $C_X$ (and similarly, between $C^{\prime}$ and $C_X$).

Proof
  • $C_X$ takes place later in the VE order than $C$, because
    • $X$ got summed out (eliminated) in $C_X$, no factor generated afterward will contain $X$ in its domain.
  • By assumption, $X$ is in the domain of $C$ + $X$ is not eliminated in $C$ $\to$ the message $\delta$ computed in $C$ must have $X$ in its domain.
  • By definition, $\beta_i(C_i) = \psi_i \cdot \prod_{k \in Nb_i} \delta_{k \to i}$, $C$’s upstream neighbor’s scope contains $X$ since its belief equals its potential multiplied by the message from $C$.

RIP and Independence

𐰃𐰠𐰆𐰢
$ \mathcal{T} $ satisfies the running intersection property if and only if, for every sepset $ S_{i,j} $, we have that $W_{<( i, j )} \text{ and } W_{< (j, i) }$ are separated in $\mathcal{H} \text{ given } S_{i,j}.$

Bethe Cluster Graph

How do we construct

Message Passing: Sum Product

VE induces a clique tree.

Given a clique tree, show how this data structure is used to perform VE.

  • caching computations $\to$ allowing multiple execution of VE to be performed.

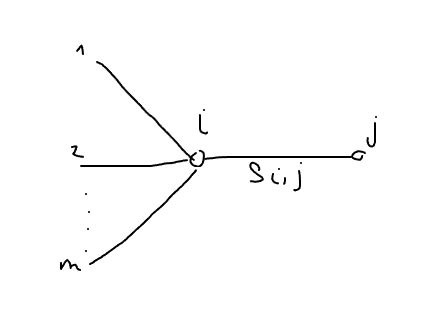
Clique-Tree Message Passing

  • $\mathcal{T}$: clique tree with cliques $C_1, \dots, C_k$.
  • $C_r$: selected root clique.
  • For each $C_i$
    • $Nb_i$: set of indexes of neighbors cliques.
    • $p_r(i)$: upstream neighbor of $i$ (parent of node $i$ in the rooted tree $\mathcal{T}$).

1. Initialize Cliques: Multiplying the factors assigned to each clique $\alpha(\phi)$, resulting in the initial potentials $$ \boxed{\psi_j(C_j) = \prod_{\phi : \alpha(\phi) = j} \phi} $$

  • Because each factor is assigned to exactly one clique, $$ \prod_{\phi} \phi = \prod_j \psi_j. $$

2. Message Passing Loop: Perform sum-product VE over the cliques

  • Starting from the leaves,
  • moving inward.
  • Each clique $C_i$, except for the root, performs a message passing computation and sends a message to its upstream neighbor $C_{p_r(i)}$.
  • Belief of Cluster: $$ \boxed{\beta_i(C_i) = \psi_i \cdot \prod_{k \in Nb_i} \delta_{k \to i}} $$
  • The message from $C_i$ to $C_j$ is computed using sum-product message passing: $$ \boxed{\delta_{i \to j} = \sum_{C_i - S_{i, j}} \overbrace{\psi_i}^{\text{init clique potential}} \cdot \overbrace{\prod_{k \in (Nb_i - \{j\})} \delta_{k \to i}}^{\text{mess from other neigbors}} } $$ In other word, $C_i$ multiplies all incoming messages from its neighbors with its initial clique potential, resulting in a factor $\psi$ whose scope is the clique, sums out all variables except those in $S_{i, j}$ and sends the resulting factor as a message to $C_j$.

3. Compute Root Belief This message passing process proceeds up the tree, culminating at root.

  • When the root clique has received all messages, it multiplies them with its own initial potential.

  • Result: beliefs factor, computed using the expression

$$ \boxed{\beta_r(C_r) = \sum_{\mathcal{X} - C_r} \prod_{\phi} \phi = \psi_r \cdot \prod_{k \in Nb(C_r)} \delta_{k \to r}} $$

$$ = \tilde{P}_{\Phi}(C_r) $$


Upward pass of variable elimination in clique tree
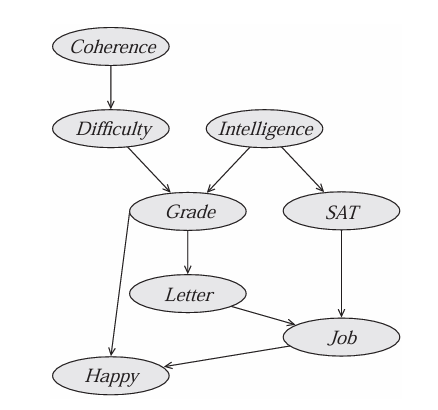
Example: simplified student network

One possible clique tree $\mathcal{T}$ for the simplified Student network

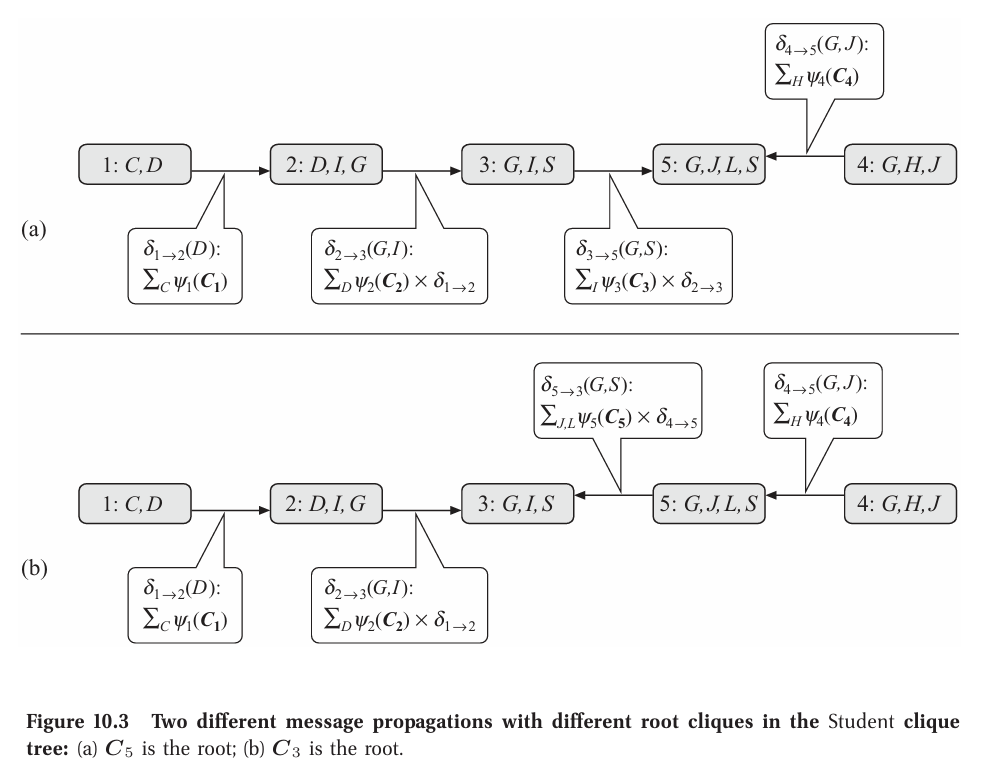
Generate a set of init potentials associated with the different cliques.

  • $\psi_i(C_i)$ is computed by multiplying the initial factors assigned to the clique $C_i$
  • For ex: $\psi_5(J, L, G, S) = \phi_L(L, G) \cdot \phi_J(J, L, S)$.

(a) Compute $P(J)$, choose some clique that contains $J$ as root clique, for ex, $C_5$.

  • some legal execution ordering: $C_1, C_2, C_3, C_4, C_5$, $C_1, C_4, C_2, C_3, C_5$.
  • illegal ordering: $C_2, C_1, C_4, C_3, C_5$.
    • because $C_2$ is ready only after it receives its message from $C_1$.

In $C_5$: $$ \beta_5(G, J, S, L) = \delta_{3\to 5}(G, S) \cdot \delta_{4 \to 5}(G, J) \cdot \psi_5(G, J, S, L) $$

Can sum out $G, L, S$ to obtain $P(J)$.

Can choose $C_4$ as root. $$ \beta_4(H, G, J) = \delta_{5\to 4}(G, S) \cdot \psi_4(G, J, S, L) $$


(b) choose $C_3$ as root. $$ \beta_3(G, S, I) = \delta_{2 \to 3}(G, I) \cdot \delta_{5 \to 3}(G, S) \cdot \psi_3(G, S, I) $$

ℹ️

Compute posterior probability

  • Pick a root in the clique tree that contain the desire variable.
  • Pass messages upward toward that root.
  • Extract marginals over variables that are in the root.
❗
  • The direction of messages depends on the root.
  • The content of each message depends on what’s below the sender $\rightarrow$ changes if the root changes.

Say, if we want to know about the posterior probability of another variable that is in a different clique $\rightarrow$ choose another root and run the procedure again.

Correctness

Prove that this algorithm,

  • when applied to a clique tree that satisfies
    • the family preservation
    • the running intersection property,
  • will compute the desire expressions over the messages and the cliques (or say the resulting beliefs (marginals) are correct).
𐰃𐰠𐰆𐰢

Assum $X$ is eliminated when a message is sent from $C_i$ to $C_j$,

Then $X$ does not appear anywhere in the tree on the $C_j$ side of the edge ($i - j$).

Proof using contradiction

Assume $X$ appears in some other clique $C_k$ that is on the $C_j$ side of the tree.

Then $C_j$ is on the path $C_i \to C_k$.

However a variable $X$ is eliminated only when a message is sent from $C_i$ to $C_j$ s.t:

  • $X \in C_i$
  • $X \not\in C_j$

$\Rightarrow$ $X$ appears in both $C_i$ and $C_k$ but not in $C_j$, violating the running intersection property.

𐰃𐰠𐰆𐰢

The message $\delta_{i \to j}(S_{i, j})$ is equal to the sum over all variables on the $C_i$-side that are not in the sepset of the product of all factors on that side

$$ \delta_{i \rightarrow j}(S_{i,j}) = \sum_{\mathcal{V} \prec (i \rightarrow j)} \prod_{\phi \in \mathcal{F} \prec (i \rightarrow j)} \phi $$

where

  • $\mathcal{F}_{\prec (i \to j)}$: all factors on the $C_i$-side of the edge.
  • $\mathcal{V}_{\prec (i \to j)}$: all variables on the $C_i$-side of the edge but are not in the sepset.

In English, “The message from clique $C_i \to C_j = $ the sum over all variables on the $C_i$-side of the edge but are not in the sepset $S_{i, j}$ of the product of all factors on the $C_i$-side of the edge.”

❗
The message $\delta_{i \to j}$ does not depend on what the root is - only on the local structure and which side of the tree the message is coming from.
Proof
$C_i$ has neighbors $C_{i_1}, C_{i_2}, \dots, C_{i_m}$ other than $C_j$.

The eliminated variables $\mathcal{V}_{\prec (i \to j)}$ in the entire subtree are:

$$ V_{\prec (i \to j)} = \left( \bigcup_{k = 1}^mV_{\prec (i_k \to j)} \right) \cup (C_i \ S_{i,j}) $$

  • The variables eliminated at each subtree rooted at $i_k$ are $\mathcal{V}_{\prec(i_k \to i)}$.
  • At $C_i$, we eliminate its local variables not in the sepset.

When we eliminate a variable at $ C_i $, it doesn’t appear in any subtree rooted at $ C_{i_k} $. So the variable sets $ \mathcal{V}_{<(i_k \to i)} $ are disjoint.

Assum $Y_i$ is eliminated at $C_i$

$$ \delta_{i \to j}(S_{i, j}) = \sum_{Y_i} \sum_{V_{\prec(i_1 \rightarrow i)}} \cdots \sum_{V_{\prec(i_m \rightarrow i)}} \left( \prod_{\phi \in F_{\prec(i_1 \rightarrow i)}} \phi \right) \cdots \left( \prod_{\phi \in F_{\prec(i_m \rightarrow i)}} \phi \right) \cdot \left( \prod_{\phi \in F_i} \phi \right) $$

$$ =\sum_{Y_i} \left( \prod_{\phi \in F_i} \phi \right) \cdot \sum_{V_{\prec(i_1 \rightarrow i)}} \left( \prod_{\phi \in F_{\prec(i_1 \rightarrow i)}} \phi \right) \cdots \sum_{V_{\prec(i_m \rightarrow i)}} \left( \prod_{\phi \in F_{\prec(i_m \rightarrow i)}} \phi \right) $$

  • This is because the variable in $ \mathcal{V}_{<(i_k \to i)} $ do not appear in any factor $\phi$ that is not from the same subtree. So their summation does not affect the other factor, and we can pull out the summation inside (exchange summation and product).

Thus,

$$ \delta_{i \to j}(S_{i, j}) = \sum_{Y_i} \psi_i \cdot \delta_{i_1 \rightarrow i} \cdots \delta_{i_m \rightarrow i} $$

Corollary

𐰃𐰠𐰆𐰢
$$ \beta_r(C_r) = \sum_{\mathcal{X} - C_r} \tilde{P}_{\Phi}(\mathcal{X}) $$

  • Because $\beta_r(C_r) = \psi_r \cdot \prod_{k \in Nb(C_r)} \delta_{k \to r}$.
    • $\prod_{k \in Nb(C_r)} \delta_{k \to r} = \sum \prod \phi$.

$\Rightarrow$ The upward pass computes correct marginals for the root.

⚠️
This proves that we can use the same clique tree to compute the probability of any variable in $\mathcal{X}$.

Sum up phần này nghĩa là nếu clique tree của mình thỏa mãn 2 tính chất … thì một message passing từ leaf đến root của nó sẽ là một legit marginal probability P~(X) …

Clique Tree Calibration

Ready Clique

$C_i$ is ready to transmit to a neighbor $C_j$ when $C_i$ has messages from all of its neighbors except from $C_j$.

Sum-product Belief Propagation

1. Initialize Cliques: $$ \boxed{\psi_j(C_j) = \prod_{\phi : \alpha(\phi) = j} \phi} $$ 2. Message Passing Loop:
simplifed student example

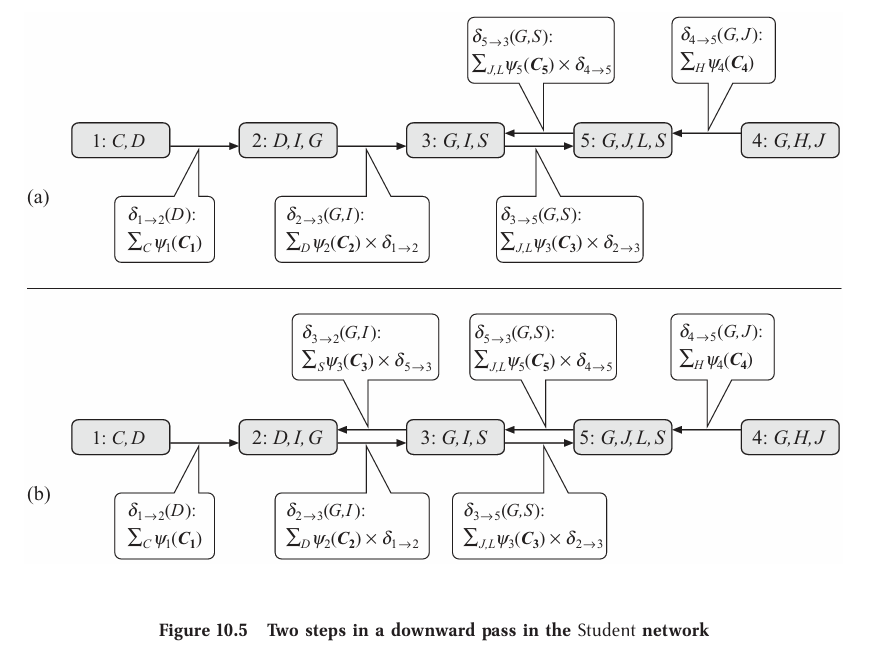
At the end of this process, all messages and clique beliefs are computed. Messages used in the computation of $\beta_i$ are precisely the same as that would have been use in the upward algorithm, thus Corollary

𐰃𐰠𐰆𐰢
$$ \beta_i(C_i) = \sum_{\mathcal{X} - C_i} \tilde{P}_{\Phi}(\mathcal{X}) $$

Calibrated

Two adjacent cliques $C_i$ and $C_j$ are said to be calibrated if $$ \boxed{\sum_{C_i - S_{i, j}} \beta_i (C_i) = \sum_{C_j - S_{i, j}} \beta_j (C_j)} $$

Cái này là belief tại cluster C_i nên vẫn bao gồm cả j, nghĩa là message từ 2 chiều vẫn khác nhau nhưng belief tại node đó sẽ = nhau nên vẫn cần tính message cả 2 chiều

Calibrated Clique Tree

𐰋𐰍𐰃𐰤
a clique tree $\mathcal{T}$ is calibrated if all pairs of adjacent cliques are calibrated.

Beliefs

clique beliefs $$ \boxed{\beta_i(C_i) = \psi_i \cdot \prod_{k \in Nb_i} \delta_{k \to i}} $$

sepset beliefs $$ \boxed{\mu_{i, j} (S_{i, j}) = \sum_{C_i - S_{i, j}} \beta_i (C_i) = \sum_{C_j - S_{i, j}} \beta_j (C_j)} $$

Clique Tree Analysis

Say we want to compute the posterior probability of all variables in the graphical models

Let $c$ be the cost of message passing to the root.

Naive message passing in clique tree: $nc$.

We can run the upward message passing algorithm once for every clique, making it the root: $Kc$.

  • $K$: number of cliques.

Using clique tree calibration:

  • Run message passing in two passes (upward pass and downward pass).
  • Compute all messages
  • The messages and beliefs in the clique tree store all necessary info about the posterior distribution.
  • Then for any clique $C_i$, compute it belief $$ \beta_i = \psi_i \cdot \prod_{k \in Nb(i)} \delta_{k \to i} $$
  • And then marginalize locally to get any variable in any clique. The cost of this algorithm is $2c$.

A Calibrated Clique Tree as a Distribution

  • A data structure that stores the results of probabilistic inference for all of the cliques in the tree.
  • An alternative representation of the measure $\tilde{P}_{\Phi}$

$$ \begin{align*} \mu_{i \to j}(S_{i,j}) &= \sum_{C_i - S_{i,j}} \beta_i(C_i) \\ &= \sum_{C_i - S_{i,j}} \psi_i \cdot \prod_{k \in Nb_i} \delta_{k \to i} \\ &= \sum_{C_i - S_{i,j}} \psi_i \cdot \delta_{j \to i} \cdot \prod_{k \in (Nb_i - \{j\})} \delta_{k \to i} \\ &= \delta_{j \to i} \cdot \sum_{C_i - S_{i,j}} \psi_i \cdot \prod_{k \in (Nb_i - \{j\})} \delta_{k \to i} \\ &= \delta_{j \to i} \cdot \delta_{i \to j} \end{align*} $$

Message Passing: Belief Update

Constructing a Clique Tree

Clique Trees from VE

Tomodachii categories sitemap