Exploiting Independence Properties

Parameterizing the Joint Distribution

Consider a simple setting:

• $X_i$ represents binary event (coin toss, yes/no COVID cause, etc) $\rightarrow$ Parameterizing the joint distribution $P(X_1, \dots, X_n)$ requires $2^n - 1$ params. (Recall)
• Assume events are marginally independent: $(X_i \perp\!\!\!\perp X_j)$ for every $i, j$. $\rightarrow$ $P(X_1, \dots, X_n) = P(X_1) \dots P(X_n)$.
  • Can use $n$ params $\theta_1, \dots, \theta_n$ to parameterize $P(X_1) \dots P(X_n)$. $$ P(X_1, \dots, X_n) = \prod_i \theta_{xi} $$
    • $\theta_{xi} = \theta_i$ if $x_i = x_i^1$,
    • $\theta_{xi} = 1 - \theta_i$ if $x_i = x_i^0$,

From $2^n - 1$ to $n$ is a dramatic reduction in the number of parameters, and the key point is:

The same applies to Conditional Indepence.

Consider a smaller picture: the joint distribution $ P(X_1, X_2, X_3, X_4) $. Using the chain rule,

$$ P(X_1, X_2, X_3, X_4) = P(X_4 \mid X_3, X_2, X_1) P(X_3 \mid X_2, X_1) P(X_2 \mid X_1) P(X_1) $$

then $ P(X_4 \mid X_3, X_2, X_1) = P(X_4 \mid X_3) $ $ \rightarrow $ # of required parameters for this CPD reduces from $ 2^3 = 8 $ to $ 2^1 = 2 $.

The joint distribution becomes

$$ P(X_1, X_2, X_3, X_4) = P(X_4 \mid X_3) P(X_3 \mid X_2, X_1) P(X_2 \mid X_1) P(X_1) $$

The total number of parameters reduces from $ 2^4 - 1 = 15 $ to $2 + 2^2 + 2 + 1 = 9$.

Bayesian Networks

• $P$ is a legal distribution:
  • $P \leq 0$ ($P$ is a product of CPDs and CPDs are non-negative).
  • $\sum P = 1$.
    Proof

    

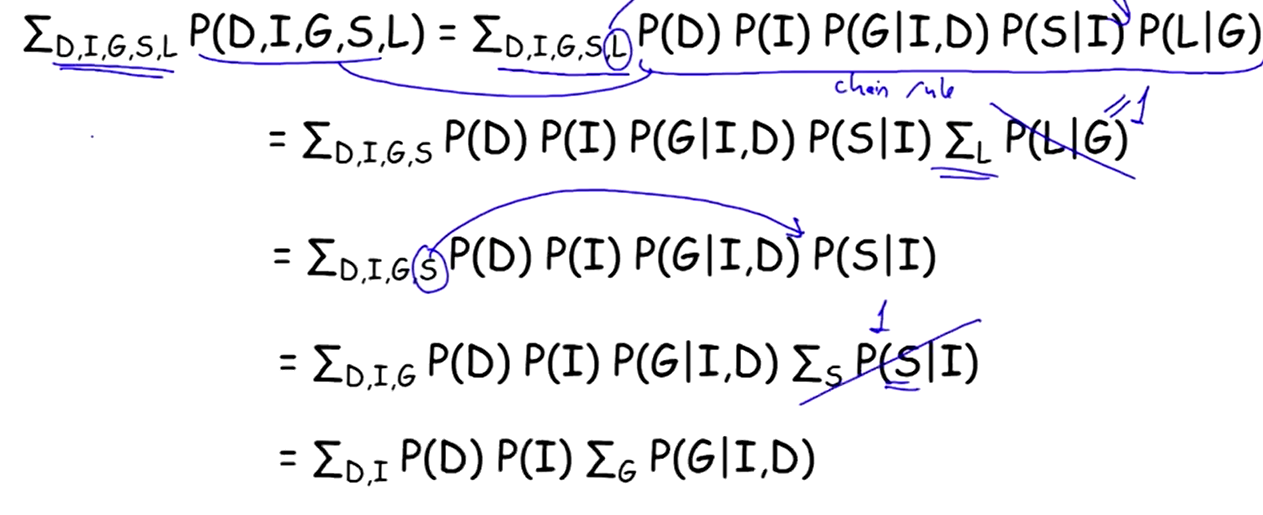
Example 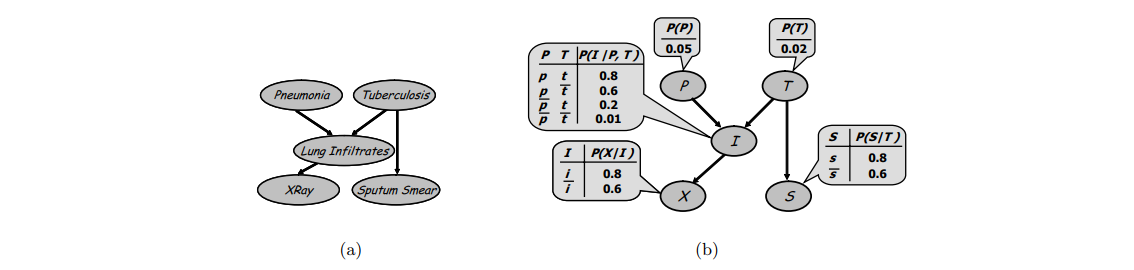(a) A simple Bayesian network showing two potential diseases, Pneumonia and Tuberculosis,

• either of which may cause a patient to have Lung Infiltrates.
• The lung infiltrates may show up on an XRay;
• there is also a separate Sputum Smear test for tuberculosis.

All of the r.v are Boolean.

(b) The same Bayesian network, together with the conditional probability tables.

Reasoning Patterns

Check this out

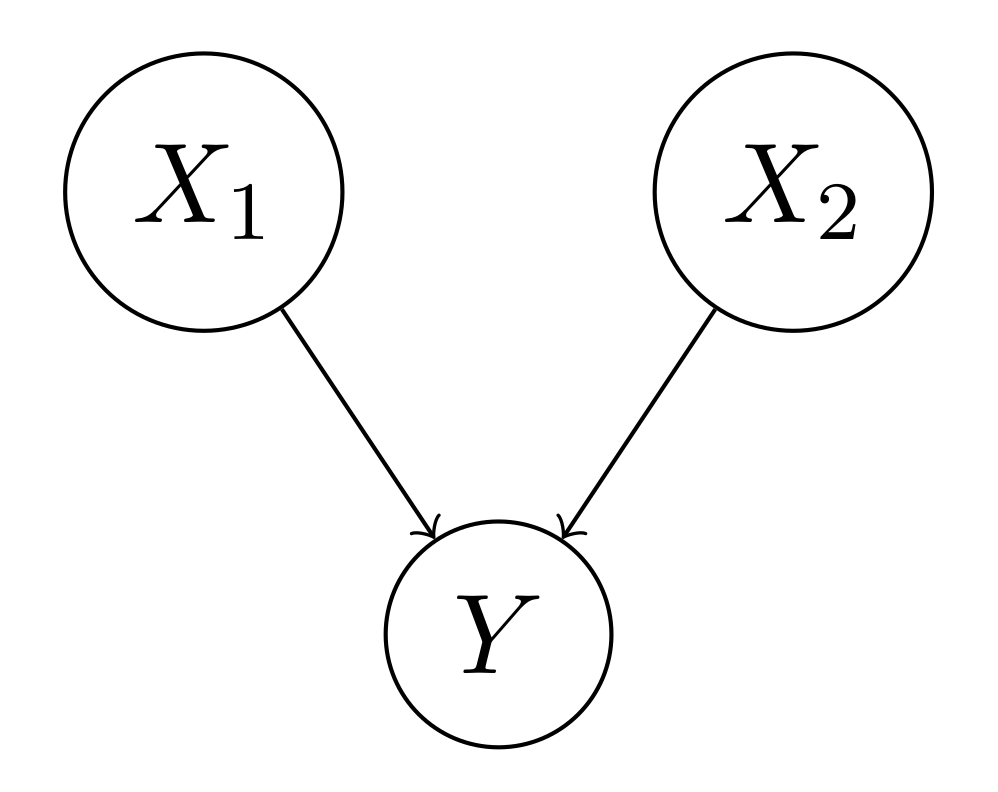
$X_1, X_2$: Causes,

$Y$: Effect.

Causal Reasoning

• $P(l^1) \approx 0.5$, the probability of a student getting the reference letter given that we know nothing about him.

We can condition on some variables (causes) and ask how that would change our probability $P(l^1)$.

• $P(l^1 \mid i^0) \approx 0.39$, if we know that the student is not so smart, the probability of him getting reference letter goes down.

• $P(l^1 \mid i^0, d^0) \approx 0.51$, if we now know that the class is easy, then the probability of the student getting high grade increases, thus he is more likely to get that refer letter.

Evidential Reasoning

Student Example

We can condition on the Grade and ask what happens to the probability of its parents or its ancestors.

• Initially,
  • $P(d^1) \approx 0.4$, the probability that the class is difficult, and
  • $P(i^1) \approx 0.3$, the probability that the student is intelligent.

But now, with the additional evidence that the student has terrible grade $g^3$,

• Evidentially,
  • $P(i^1 \mid g^3) \approx 0.08$, the probability that the student is intelligent goes down, but
  • $P(g^1 \mid g^3) \approx 0.08$, the probability that the class is difficult goes up as well.

Intercausal Reasoning

Student Example

Say, if a student gets low grade, he might not be so smart

• $P(i^1 \mid g^3) \approx 0.079$.

On the other hand, if we now discover that the class is hard,

• $P(i^1 \mid g^3, d^1) \approx 0.11$, the probability that the student is smart slightly increases.

$\rightarrow$ we have explained away the poor grade via the dificulty of the class.

Example 2:

We have fever and a sore throat, and are concerned about mononucleosis.

Doctor then tells us that we have flu.

Having the flu does not prohibit us from having mononucleosis. Yet, having the flu provides an alternative explanation of our symptoms, thereby reducing substantially the probability of mononucleosis.