Chapter 9 (Pt. 1): Exact Inference - Queries
PGMs represent joint probability distributions over a set of variables $\mathcal{X}$. Let’s use this representation to answer actual queries.
Queries
A query over a graphical model asks to compute simple statistics over the function such as its minimum or average value.
Conditional Probability Queries
Given: Variables $\mathcal{X}$, Evidence $E = e$, Query $Y$.
Task: Compute $P(Y \mid E = e)$.
$$ \boxed{P(Y \mid E = e) = \frac{P(Y, e)}{P(e)}} $$
Let $W = \mathcal{X} - Y - E$ be variables that are neither query nor evidence (hidden variables).
$$ \boxed{P(Y, E = e) = \sum_{W} P(Y, E = e, W)} $$
$$ \boxed{P(e) = \sum_{Y, W} P(Y, E = e, W) = \sum_Y P(Y, E = e)} $$
Reduce factors
Reduce the factors by evidence $E = e$.
- computational optimization: preprocess the factor to remove irrelevant entries instead of keeping the full factor and evaluating it every time with evidence fixed.
- Reducing factors is just plug-in + table simplification.
The sum can grow exponentially in the number of hidden variable.
Example
- $\mathcal{X} = \{X_1, \dots, X_5\}$, $X_i$ is binary variable.
- Evidence $E = {X_1 = 1}$.
- Query $Y = X_2$.
- $W = \mathcal{X} - Y - E = \{X_3, X_4, X_5\}$.
$$ P(Y = y, E = e) = \sum_{x_3, x_4, x_5} P(Y = y, X_1 = 1, \underbrace{X_3 = x_3, X_4 = x_4, X_5 = x_5}_{W}) $$
$\rightarrow$ Compute the joint probability for all 8 possible assignments of $x_3, x_4, x_5$.
In case of 20 variables? $2^{20}$.
Examples
Conditional probability inferences are often called Sum-Product: Sum over a product of factors.Student Example
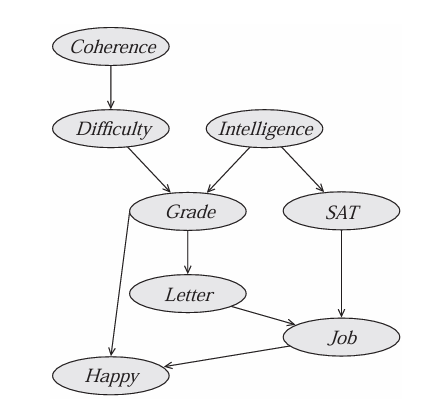
$$ P(J) = \sum_{C,D,I,G,S,L,H} \phi_C(C) \phi_D(C,D) \phi_I(I) \phi_G(G,I,D) \phi_S(S,I) \phi_L(L,G) \phi_J(J,L,S) \phi_H(H,G,J) $$
Observe evidences $I = i$ and $H = h$, plug in the original factors. $$ P(J \mid I = i, H = h) = \sum_{C,D,G,S,L} \phi_C(C) \phi_D(C,D) \phi_I(i) \phi_G(G,i,D) \phi_S(S,i) \phi_L(L,G) \phi_J(J,L,S) \phi_H(h,G,J) $$

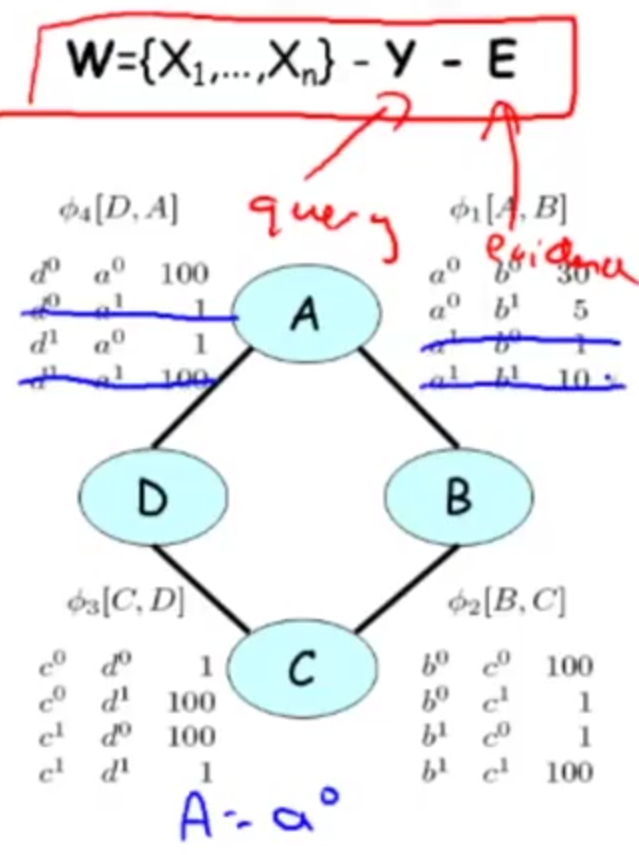
$$ \tilde{P}(D) = \sum_{ABC} \phi_1(A, B) \times \phi_2(B, C) \times \phi_3(C, D) \times \phi_4(A, D) $$
Observe $A = a^0$, reduce factors by removing rows that are inconsistent with the observed evidence. $$ \tilde{P}(D, A = a^0) = \sum_{ABC} \phi^{\prime}_1(A = a^0, B) \times \phi_2(B, C) \times \phi_3(C, D) \times \phi^{\prime}_4(A = a^0, D) $$
Maximum a Posteriori (MAP)
Given: Variables $\mathcal{X}$, Evidence $E = e$, Query $Y = \mathcal{X} - E$.
Task: Compute $\text{MAP}(Y \mid E = e) = \text{argmax}_yP(Y = y \mid E = e)$.
- There might be more than one possible solution.
Max-Product
$$ P(Y \mid E = e) = \frac{P(Y, e)}{\underbrace{P(e)}_{\text{constant w.r.t Y}}} \propto P(Y, E = e) $$
$$ \begin{align*} P(Y, E = e) &= \frac{1}{\underbrace{Z}_{\text{const}}} \prod_k \phi^{\prime}_k(D^{\prime}_k) \\ &\propto \prod_k \phi^{\prime}_k(D^{\prime}_k) \end{align*} $$
$$ \boxed{\text{argmax}_Y P(Y \mid E = e) = \text{argmax}_Y \prod_k \phi^{\prime}_k (D^{\prime}_k)} $$