-
CDF $F_X$ “accumulate” probability “up to” x.
-
Think of CDF as running a sliding window across PMF and adding up the probabilities associated with each outcome as that window passes by.
Lecture 5 + 6 + 7: Discrete Random Variables
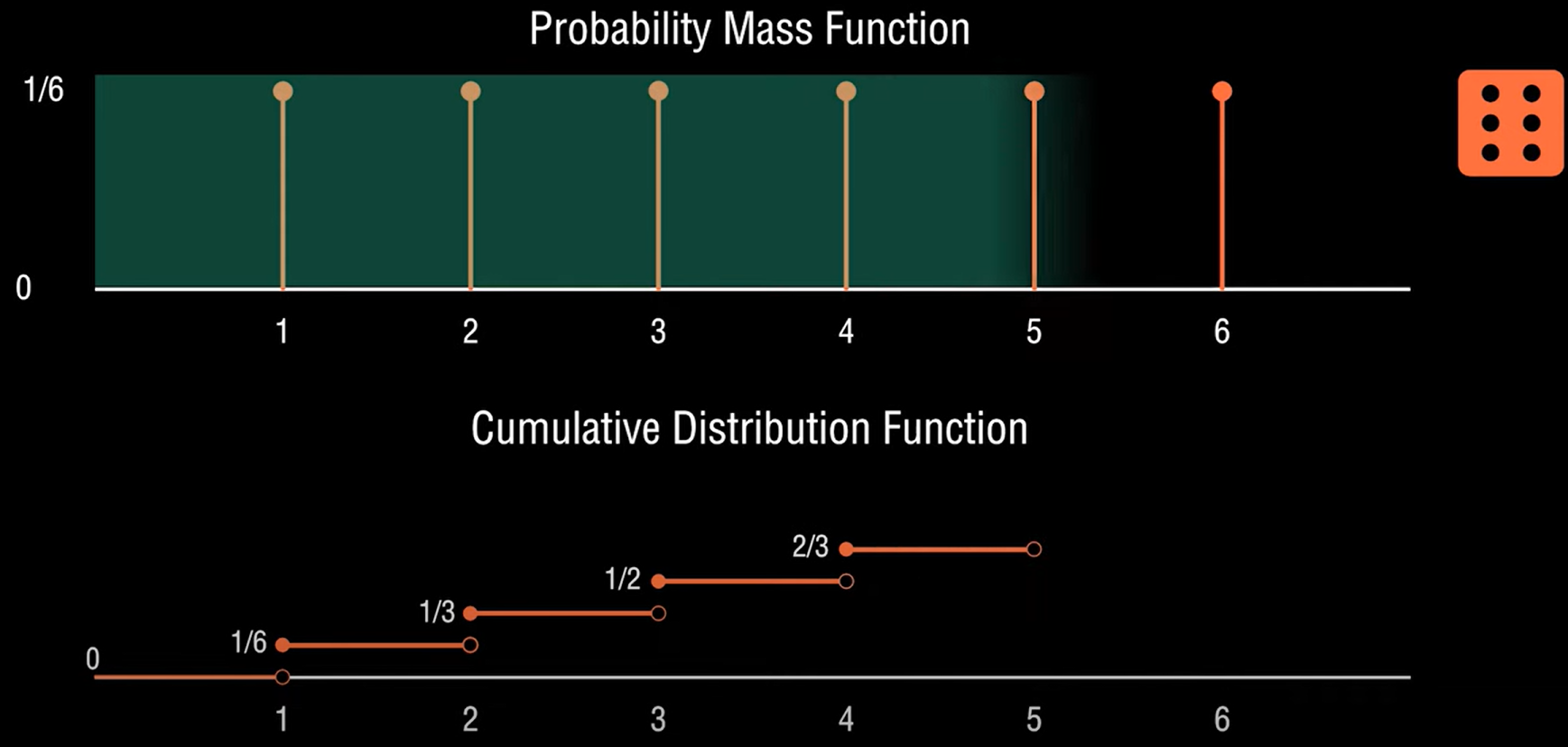
Cumulative Distribution Function
- Another method to describe the distribution of random variables.
- Advantage: Can be defined for any kind of random variable (discrete, continuous, and mixed).
The CDF of discrete random variable $X$:
$$
F_X(x) = P(X \leq x) = \sum_{k \leq x}p_X(k), \quad \text{for all } x \in \mathbb{R}
$$
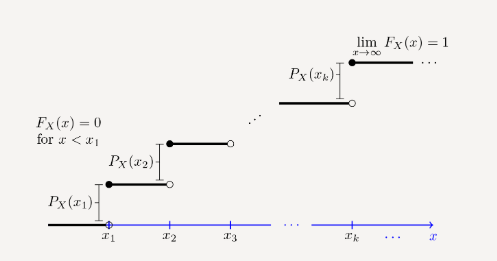
Properties of CDF
piecewise constant and staircase-like form.
-
$F_X$ is monotonically nondecreasing: $$ \text{if } x \leq y \text{, then } F_X(x) \leq F_X(y). $$
-
$F_X$ tends to 0 as $x \to -\infty$, and to 1 as $x \to \infty$.
-
for all $x_k \in R_x = \{x_1, x_2, \dots\}$ $$ \boxed{F_X(x_k) = \sum_{x_k = -\infty}^{x}p_X(x_k)} $$
$$ \boxed{p_X(x_k) = P(X \leq x_k) - P(X \leq x_k - 1) = F_X(x_k) - F_X(x_k - 1)} $$
proof for (2)
By the axiom of probability, $$ \lim_{x\to+\infty}F_X(x) = 1. $$ Using complement rule, $$ P(X > x) = 1 - P(X \leq x) = 1 - F_X(x). $$ Recall $$ P(X \in \mathbb{R}) = 1. $$ Thus, $$ \lim_{x \to -\infty} 1 - F_X(x) = P(X > -\infty) = 1 \text{ (Because X is always in some real-valued range)} $$
$$ \Leftrightarrow \lim_{x \to -\infty} F_X(x) = 0. $$
CDF jumps at each point in the range $\rightarrow$ stays flat between $x_k$ and $x_{k + 1}$. $$ F_X(x) = F_X(x_k), \text{ for } x_k \leq x < x_k + 1. $$
Jumps in the CDF correspond to points $x$ for which $P(X = x) > 0$.
Useful formulas
$P(a < X \leq b)$
For all $a \leq b$, $$ \boxed{P(a < X \leq b) = P(X \leq b) - P(X \leq a) = F_X(b) - F_X(a)} $$
$P(X \leq x)$
CDF gives us $P(X \leq x)$. To find $P(X < x)$, for a discrete random variable $$ \boxed{P(X < x) = P(X \leq x) - P(X = x) = F_X(x) - P_X(x)} $$
$<$ and $\leq$ could make a difference in the case of discrete random variables.
Quantiles
CDF $F$ is strictly monotonically increasing + $F$ is bijective
- Injective (one-to-one): $f(x_1) = f(x_2) \Rightarrow x_1 = x_2$.
- Surjective (onto): The range of $f$ covers the entire domain.
$\Rightarrow$ it has an inverse, called inverse cdf, or percent point function (ppf), or quantile function.