Definitions

Graphs

$ G = (V, E) $

• $ V $: non empty set of vertices (or nodes)
• $ E $: edges; set of two-element subsets of $ V $.

Adjacent

Two nodes $ x_i $ and $ x_j $ are adjacent if $ \{ x_i, x_j \} \in E $.

Incident

An edge $ e = \{ x_i, x_j \} $ is incident to $ x_i, x_j $.

Degree of a Node

The # of edges incident to a node.

Simple Graph

• No self-loops or multiple edges (a.k.a multiedge).
• No directed edges.

Matching Problems

Sex Example

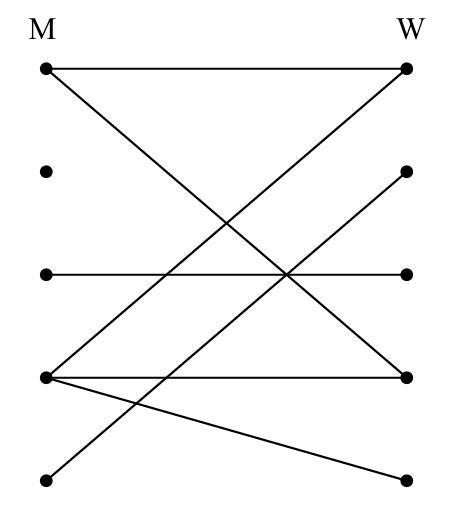
• US population $ | V | $
  • $ | M |, | F | $: male, female.

Let alone exactly which couples are adjacent, only need to figure out the relationship bw the average number of partners per male and per female.

Every edge is incident to exactly one M and one F $ \Rightarrow $ sum of the degrees of the M vertices = # of edges ($ | E | $) = sum of the degrees of the F vertices $$ \sum_{x \in M} \deg (x) = |E| = \sum_{y \in F} \deg (y) $$

• Avg # of opposite-gender partners for male $ A_m = \frac{\sum_{x \in M} \deg(x)}{|M|} = \frac{|E|}{|M|} $.
• Avg # of opposite-gender partners for female $ A_m = \frac{\sum_{y \in F} \deg(x)}{|F|} = \frac{|E|}{|F|} $.

The Handshaking Lemma

The sum of degrees of the vertices in a graph equals twice the number of edges.

Proof: Every edge contributes two to the sum of the degrees, one for each of its endpoints.

Coloring

Exam Scheduling Example

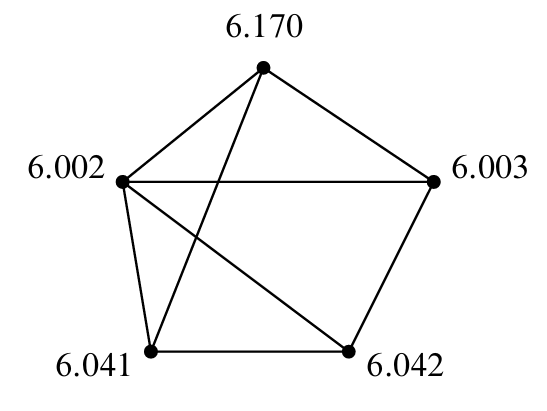
Assign time slot for final exam

• some students are taking several classes with finals
• a student can take only one test during a particular time slot
• adjacent vertices: some student is taking both courses
  • 6.002 and 6.042 cannot have an exam at the same time since there’re student in both courses.

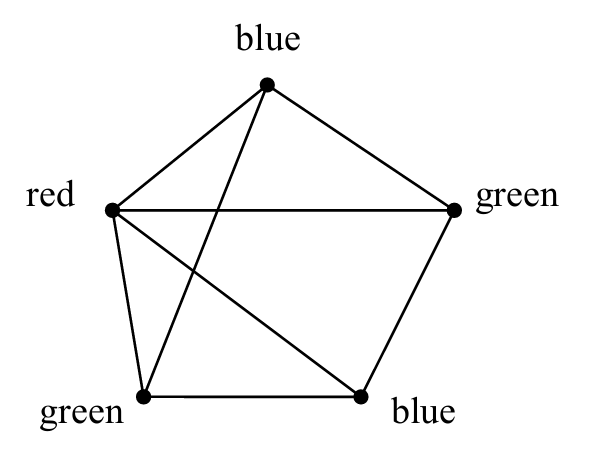
Slots

• blue: 6 - 8
• red: 9 - 11
• green: 13 - 15

Can’t do 2-coloring bc 6.002 - 6.170 - 6.041 forms a triangle and each one of these guys has to be different than the other two.

Chromatic number

$ \mathcal{X}(G) $: The minimum value of $ K $ for which $ G $ has a valid $ k $-coloring

Basic Algorithm (Greedy Color Algorithm)

Proof: By induction

Induction Hypothesis: $ P (n) = n$-node graph with maximum degree $ d $ is $ (d + 1) $-colorable

Base case: $ n = 1 \Rightarrow $ 0 edges, $ d $ = 0, 1 color = $ d $ + 1.

Inductive step: Assume $ P(n) $ is true for induction

Let

• $ G = (V, E) $ be any $ (n + 1) $-node graph
• $ d = $ max degree in $ G $.

Want to show: We can color it using $ d + 1 $ colors

Order the nodes $ V_1, V_2, \dots , V_n, V_{n + 1} $

Remove the $ V_{n + 1} $ from $ G $ to create $ G^{\prime} = (V^{\prime}, E^{\prime}) $

$ G^{\prime} $ has max degree $ \leq d $ and it has $ n $ nodes, so $ P(n) $

Says Basic Alg uses $ \leq d + 1 $ colors for $ V_1, V_2, \dots, V_n $