Parameters Estimation

What are Parameters?

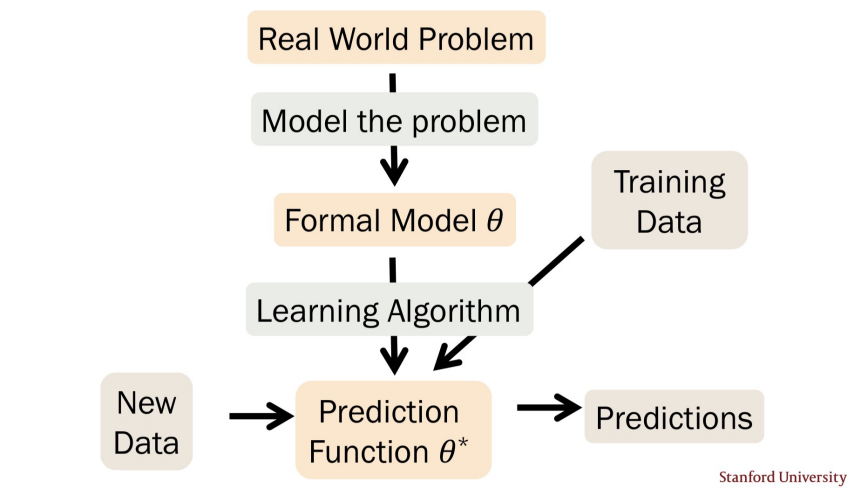
Parametric models: Given model, params yield actual distribution

• $\theta$ can be a vector of params.

Maximum Likelihood with Poisson

IID (Independent and Identically Distributed) rv $X_1, \dots, X_n$

$X_i \sim \text{Poi}(\lambda)$

1. PMF: $$f(x_i \mid \lambda) = \frac{e^{-\lambda}\lambda^{x_i}}{x_i!}$$
2. Likelihood of all the data (given a particular $\lambda$): $$ \begin{align*} L(\lambda) &= f(x_1 \dots x_n \mid \lambda)\\ &= \prod_{i = 1}^{n} f(x_i \mid \lambda) \quad \text{(IID)}\\ &= \prod_{i = 1}^n \frac{e^{-\lambda}\lambda^{x_i}}{x_i!} \end{align*} $$

The log’s gonna go live inside the house and break down the columns as it goes there. $$ LL(\lambda) = \log\prod_{i = 1}^n \frac{e^{-\lambda}\lambda^{x_i}}{x_i!} = \sum_{i = 1}^n \log \frac{e^{-\lambda}\lambda^{x_i}}{x_i!} = \boxed{ \sum_{i = 1}^n - \lambda + x_i \, \log{\lambda} - \log{x_i!} } $$

We want to choose the $\lambda$ to make this expression as large as possible $\rightarrow argmax$ of this log-likelihood.

4. Differentiate w.r.t. $\lambda$, and set to 0: $$ \frac{\partial LL(\lambda)}{\partial \lambda} = \sum_{i=1}^{n} \left( -1 + \frac{x_i}{\lambda} \right) = -n + \frac{1}{\lambda} \sum_{i=1}^{n} x_i $$

$$ \Leftrightarrow 0 = -n + \frac{1}{\lambda} \sum_{i=1}^{n} x_i \Leftrightarrow \lambda = \frac{1}{n} \sum_{i=1}^{n} x_i $$

Maximum Likelihood with Bernoulli

$D = [0, 1, 0, 0, 1, \dots, 0]$

IID (Independent and Identically Distributed) rv $X_1, \dots, X_n$

$X_i \sim \text{Ber}(p)$

What is $\theta_{MLE} = p_{MLE}$?

1. Determine formula for $LL(\theta)$ $$ LL(\theta) = \sum_{i = 1}^{n} \log f(X_i \mid p) $$ with $$ f(X_i \mid p) = \begin{cases} p, & \text{if } X_i = 1 \\ 1 - p, & \text{if } X_i = 0 \end{cases} $$ Wait, this is very cute and helpful but it’s not at all differentiable? Let’s see Chris Piech’s slickiest trick!

Optimization (argmax)

Gradient Descent

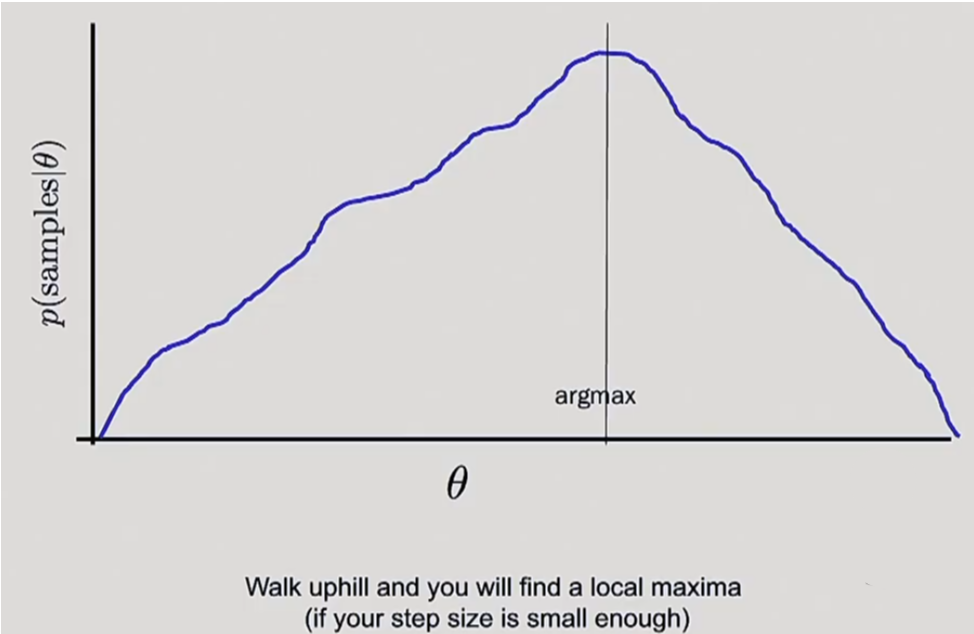
Calculate deriviative of the likelihood given every $\theta$ for the blue curve would be too computationaly expensive.

• Start with any $\theta$.
  • look at the likelihood of your $\theta$ $\rightarrow$ look at the deriviative at that point to see which way to go.
  • can’t see the whole curve.

We don’t care abt the likelihood, we care abt the $\theta$ that gives the likelihood.