Lecture 1: Introduction to Algorithms

Steven Skiena dsa

What is an Algorithm?

  • A procedure that takes any of the possible input instances and transforms it to the desired output.
  • Must solve a general, well specified problem.
    • An algorithmic problem is specified by describing the complete set of instances.
ℹ️

We seek algorithms which are

  • correct
  • efficient

Correctness

  • Always returns the desired output for all legal instances of the problem.
  • Correct algorithms usually come with a proof of correctness.

Robot Tour

  • Problem: Robot Tour Optimization
  • Input: A set $ S $ of $ n $ points in the plane.
  • Output: Shortest cycle tour that visits each point in the set $ S $.

NearestNeighbor(P)
    Choose an initial point p0 from P
    Mark p0 as visited
    path = [p0]
    current = p0

    While there are unvisited points in P
        next = the closest unvisited point to current
        Mark next as visited
        Add next to path
        current = next

    Add p0 to path to complete the cycle
    Return path
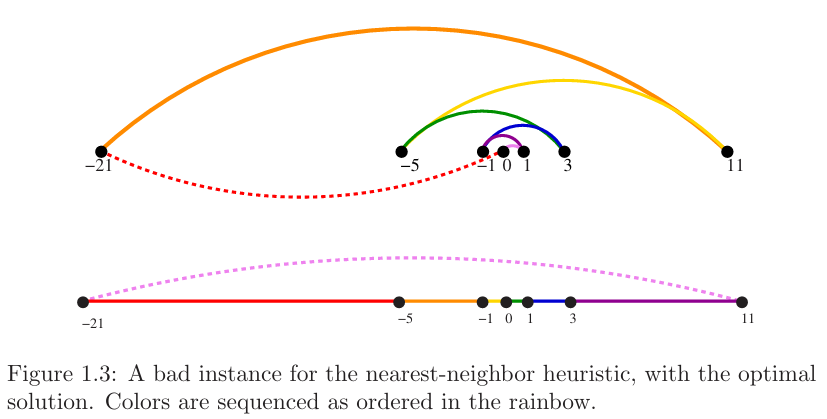
The algorithm always finds a tour, but it doesn’t necessarily find the shortest possible tour.

Exhaustive Search: Try all possible orderings of the points, then select the one which minimizes the total length.

d = INFINITY
For each of the factorial(n) permutations p_i of the n points
    If (cost(p_i) <= d)
    then d = cost(p_i) and p_min = p_i
Return p_min

Since all possible orderings are considered $ \righarrow $ guaranteed to end up with the shortest possible tour.

  • However, for 20 points, a computer must enumerate all 20! orderings.

Selecting the Right Jobs

  • Problem: Movie Scheduling Problem
  • Input: A set I of n intervals on the line.
  • Output: What is the largest subset of mutually non-overlapping intervals that can be selected from I?

An instance of non-overlapping movie scheduling problem. Red titles: optimal solution.

  • Accept the earliest starting job first: might block us from taking many other jobs if that first job is long.
  • Accept the shortest job and keep seeking the shortest available job: War and Peace is both the first job available and long enough to kill off all other prospects.

Reasoning about Correctness

We need tools to distinguish correct algorithms from incorrect ones, the primary one of which is called a proof.

  1. a clear, precise statement of what you are trying to prove.
  2. a set of assumptions of things that are taken to be true, and hence can be used as part of the proof.
  3. a chain of reasoning that takes you from these assumptions to the statement you are trying to prove.
  4. a little square (QED) at the bottom to denote that you have finished: “thus it is demonstrated.”

Problems and Properties

Problem

  1. a set of allowed input instances.
  2. the required properties of the algorithm’s output.
❗
It is impossible to prove the correctness of an algorithm for a fuzzily stated problem.

Demonstrating Incorrectness

Find an instance on which it yields an incorrect answer (counterexample).

  • Verifiability
    • Calculate what answer the algorithm will give in this instance, and
    • display a better answer so as to prove that the algorithm didn’t find it.
  • Simplicity.

Techniques

  • Think small.
    • Small examples are easy to verify and reason about.
  • Think exhaustively.
  • Hunt for the weakness.
    • “always take the biggest” (greedy).
  • Go for a tie.
    • break heuristic: provide instances of same size.
      • the heuristic has nothing to base its decision on.
  • Seek extremes
    • hugh and tiny, left and right, few and many, near and far.

Induction and Recursion

  • Failure to find a counterexample to a given algorithm does not mean “it is obvious” that the algorithm is correct.
  • A proof or demonstration of correctness is needed.
ℹ️
Recursion = Mathemathical Induction in action $ \rightarrow $ used to verify the correctness of a recursive or incremental insertion algorithm.
Increment Example 
Increment(y):
    if y == 0:
        return 1
    else if y mod 2 == 1:
        return 2 * Increment(⌊y / 2⌋)
    else:
        return y + 1

Base case

  • y = 0, Increment(0) = 1
  • 0 + 1 = 1

So Increment(0) = 0 + 1, thus P(0) holds


Inductive Step (Strong Induction Hypothesis) Assume that $ P(k) $ holds for all $ k < y $,

  • for all natural numbers less than y, assume $ Increment(k) = k + 1 $.

Must show that $ P(y) $ holds: $ Increment(y) = y + 1 $


Case 1: $ y $ is even

Let $ y = 2m, \text{ for some } m \in \mathbb{N} $, then

  • $ Increment(2m) = 2m + 1 $

Thus $ Increment(y) = y + 1 $ (desired result)

Case 2: $ y $ is odd

Let $ y = 2m + 1 $ for some integer $ m $, then

$$ \begin{align*} Increment(\lfloor 2m + 1 \rfloor) &= 2 * Increment(\lfloor m + 1/2 \rfloor) \\ &= 2 * Increment(m) &= 2 * (m + 1) = 2m + 2 = y + 1 \end{align*} $$

Thus $ Increment(y) = y + 1 $

Proof by Contradiction

  • Assume that the hypothesis is false.
  • Develop some logical consequences of this assumption.
  • Show that one consequence is demonstrably false, thereby showing that the assumption is incorrect and the hypothesis is true.
Euclid's proof that there are infinite number of prime numbers that have no non-trivial factors, only 1 and itself

Prime numbers: 2, 3, 5, 7, 11, …

Assume that there are only a finite $ m $ number of primes: $ p_1, \dots, p_m $

The integer formed as the product of “all” the listed primes: $$ N = \prod_{i =1}^{m} p_i $$

  • $ N $ is divisible by any of known primes.
  • Consider $ N + 1 $
    • If $ p_i $ divides both $ N \text{and} N + 1 $, then it must divide their difference: $$ (N + 1) - N = 1 $$

Since no prime divides 1, $ N + 1 $ is a prime itself

  • However, it is missing from the list of $ m $ all known primes (contradiction).

Thus there cannot be a bounded number of primes.

Modeling the Problem

The art of formulating your application in terms of precisely described, well-understood problems.

Formulate Problem in terms of computing properties of common structures

  • Permutations: arrangements, or ordering of items
    • {1, 2, 3, 4} and {4, 3, 2, 1}: 2 distict permutations of the same set of four integers.
    • “arrangement”, “tour”, “ordering”, “sequence”.
  • Subsets: selections from a set of items.
    • Ex: {1, 2, 3} and {2}
    • Order does not matter: {1, 2, 3} = {3, 2, 1}.
    • “cluster”, “collection”, “committee”, “group”, “packaging”, “selection”.
  • Trees: hierarchical relationship between items.
    • “hierarchy”, “dominance relationship”, “ancestor/descendant relationship”, “taxonomy”.
  • Graphs: relationships between arbitrary pairs of objects.
    • “network”, “circuit”, “web”, “relationship”.
  • Points: locations in some geometric space.
    • “sites”, “positions”, “data records”, “location”.
  • Polygons: regions in some geometric spaces.
    • “shapes”, “regions”, “configurations”, “boundaries”.
  • String: sequences of characters, or patterns.
    • “text”, “characters”, “patterns”, “labels”.

Recursive Objects

  • Decomposition rules
  • Basis cases
    • the specification of the smallest and simplest objects where the decomposition stops.
Tomodachii categories sitemap